0. 堆的定义
以下引自《算法导论》:
堆(Heap)是一个可以被看成近似完全二叉树的数组。树上的每一个结点对应数组的一个元素。除了最底层外,该树是完全充满的,而且是从左到右填充。堆包括最大堆和最小堆:最大堆的每一个节点(除了根结点)的值不大于其父节点;最小堆的每一个节点(除了根结点)的值不小于其父节点。
实现堆的方式有很多,最简单的就是采用完全二叉树来实现,我们称其为二叉堆,这种方式实现简单,但是效率一般。更高效的实现有斐波那契堆等,各种不同的实现比较请参考维基百科。
本文讲解如何通过完全二叉树来实现一个大顶堆。以大顶堆为例,其满足下列性质:
- 它是一棵完全二叉树
- 树中的任意非空节点的值总是大于等于其孩子节点的值
大顶堆示意图:
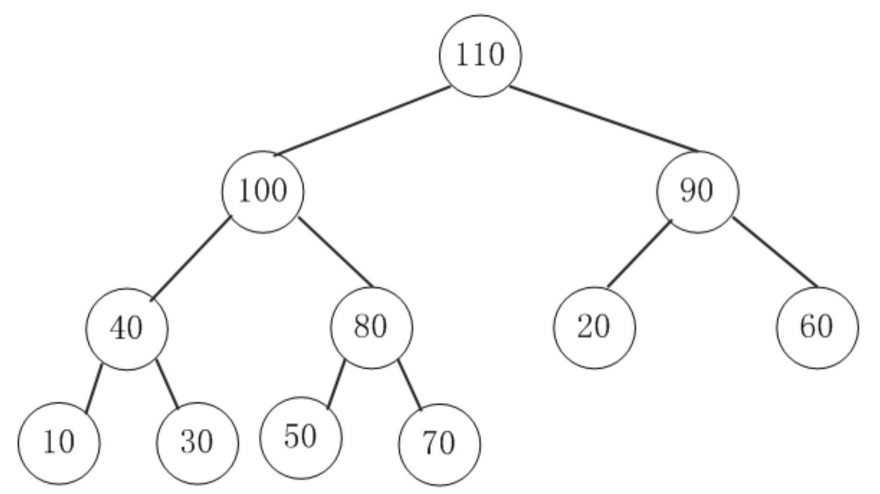
1. 常见操作
1.1. 外部操作
- peek:取出堆顶元素
- push:向堆中插入一个元素
- pop:返回堆顶元素,并将堆顶元素删除
- remove(i):删除并返回堆中指定下标为 i 的元素
- size:获取堆中元素个数
- isEmpty:判断堆是否为空
- init:由一个普通数组初始化成一个堆结构性质的数组
1.2. 内部操作
- heapifyUp:由下至上调整
- heapifyDown:由上至下调整
2. 实现
首先,二叉堆一般是通过数组来实现。假设第一个元素在数组中的索引为0,则父节点和子节点的位置关系如下:
- 索引为i的左孩子的索引为 2×i+1
- 索引为i的右孩子的索引为 2×i+2
- 索引为i的父节点的索引为 (i-1)/2
如下图所示:
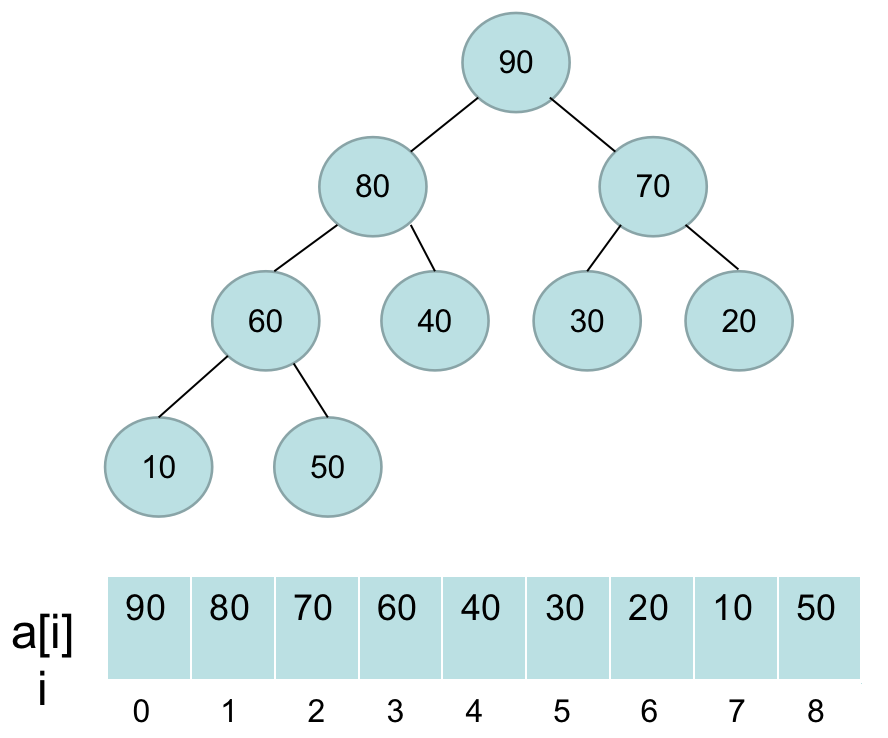
2.1. 插入操作
当插入一个元素的时候,首先将其放置在数组的末尾,然后逐步向上调整,使整棵树重新满足堆的性质。这里的向上调整,指的是,将新插入的元素与其父节点进行比较,如果其值大于父节点的值,则交换两者的位置。如此迭代,直到该节点变为根节点或者其值不在大于父节点。
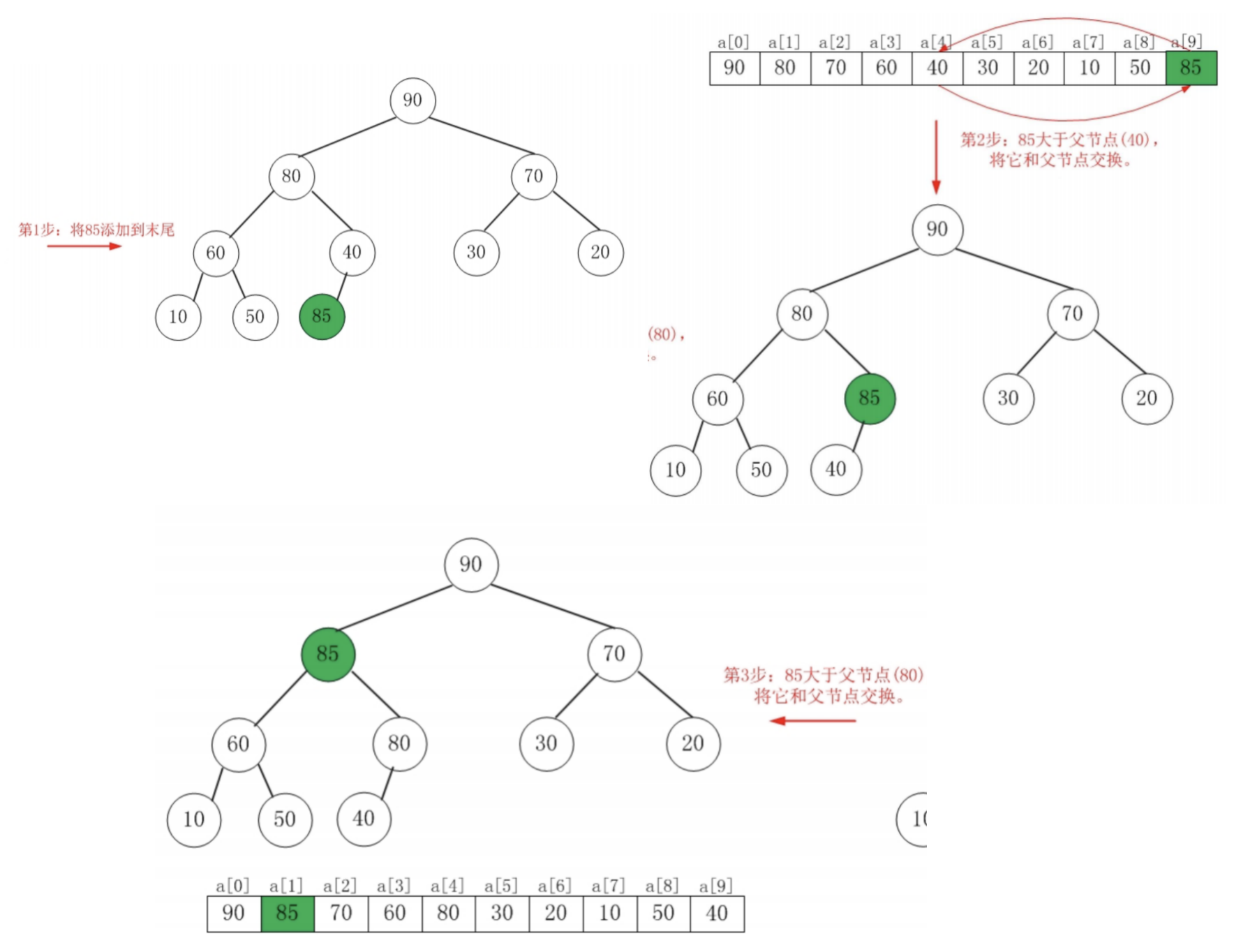
2.2. 删除操作
当删除堆顶元素时,首先将堆尾元素替换至堆顶,这就相当于把堆顶元素删除了。随后,从堆顶元素开始,由上至下调整堆结构,使其重新满足堆的结构。
这里的向下调整,指的是,将父节点与其两个孩子节点进行比较,并与较大的孩子节点进行交换,逐层向下。
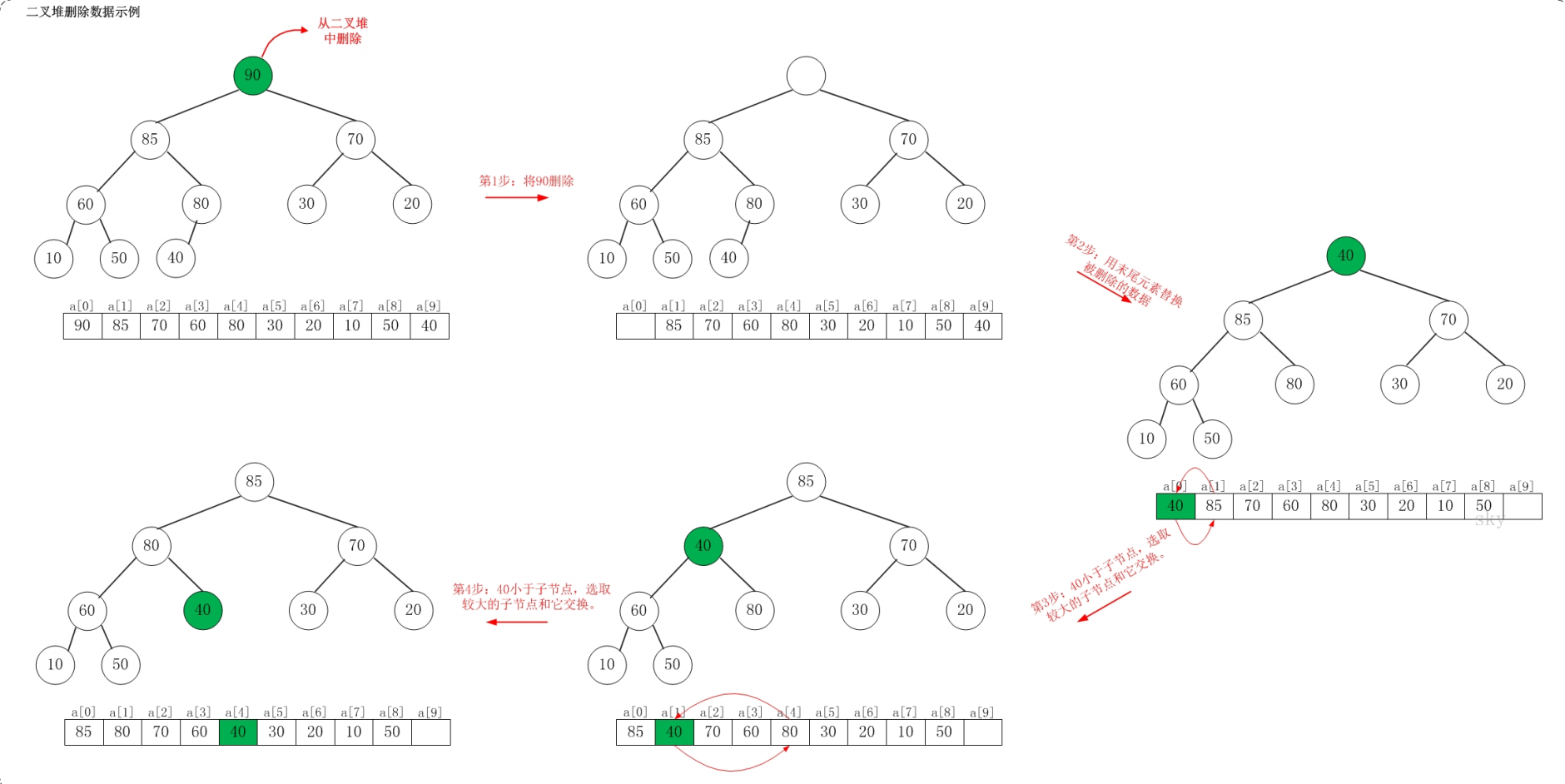
2.3. 初始化
初始化操作将一个普通数组转化成符合堆性质的数组。对于一个原始的二叉堆,从最后一个非空节点(即下标为 (n-1)/2 )开始,逐个向下调整,从而使得整个二叉堆满足大顶堆的性质。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
|
package main
import (
"fmt"
)
type MaxHeap []int
func (h *MaxHeap) Peek() int {
return (*h)[0]
}
func (h *MaxHeap) Pop() int {
x := (*h)[0] // 取出堆顶元素
n := len(*h)
h.swap(0, n-1) // 将堆尾元素调整至堆顶
*h = (*h)[:n-1] // 删除末尾节点
h.heapifyDown(0, len(*h)) // 由上至下调整
return x
}
func (h *MaxHeap) Push(x int) {
*h = append(*h, x)
h.heapifyUp(h.Size() - 1)
}
func (h *MaxHeap) Size() int {
return len(*h)
}
func (h *MaxHeap) IsEmpty() bool {
return h.Size() == 0
}
// 将普通的数组调整至符合堆性质
func (h *MaxHeap) Init() {
n := h.Size()
// 从最后一个非叶节点开始逐个向下调整
for i := (n - 1) / 2; i >= 0; i-- {
h.heapifyDown(i, n)
}
}
// 0 ≤ i < n
func (h *MaxHeap) Remove(i int) int {
n := h.Size()
if i == n-1 { // 如果删除的是最后一个元素,则不需要调整
x := (*h)[i]
*h = (*h)[:n-1]
return x
}
x := (*h)[i]
h.swap(i, n-1)
*h = (*h)[:n-1]
h.heapifyDown(i, len(*h))
return x
}
func (h *MaxHeap) heapifyDown(i, n int) {
for {
left, right := 2*i+1, 2*i+2
j := left // j 表示待交换的孩子节点
// 判断节点i是否有孩子节点
if left >= n || left < 0 { // left < 0 after int overflow
break
}
// 如果右节点存在,并且右节点的值更大
if right < n && (*h)[right] > (*h)[left] {
j = right
}
// 如果父节点i的值大于孩子节点的值,说明不需要交换
if (*h)[i] > (*h)[j] {
break
}
// swap
h.swap(i, j)
i = j // 向下一层
}
}
func (h *MaxHeap) heapifyUp(i int) {
for {
parent := (i - 1) / 2
if parent < 0 || (*h)[parent] >= (*h)[i] {
break
}
h.swap(i, parent)
i = parent // 向上一层
}
}
func (h *MaxHeap) swap(i, j int) {
(*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}
func main() {
maxHeap := MaxHeap{1, 3, 5, 4, 2, 7}
maxHeap.Init()
maxHeap.Remove(1) // remove 4
fmt.Printf("top:%d\n", maxHeap.Peek())
fmt.Printf("%v\n", maxHeap)
//maxHeap.Push(9)
//maxHeap.Remove(0)
for !maxHeap.IsEmpty() {
fmt.Printf("%d ", maxHeap.Pop())
}
}
|
从代码可以看出,最主要的逻辑就是heapifyDown(),heapifyUp()这两个函数。理解了这个调整的过程,堆的原理就不难理解了。
参考:
- https://en.wikipedia.org/wiki/Heap_(data_structure)
- https://golang.org/src/container/heap/heap.go



